Раздел сайта
Новости
Опрос
Определение осадки фундаментов зданий с учетом консолидации грунтовых оснований
Опубликовано: 02.09.2018
В статье представлены разработанные на основе теории наследственной ползучести Больцмана (Boltzmann L.) – Вольтерра (VolterraV.) математическая модель и приближенный аналитический метод определения осадки фундаментов зданий с учетом консолидации грунтовых оснований.
This article describes a mathematical model and an approximate analytical method for determining foundation settlement taking into account consolidation of soil bases. The method was developed on the basis of the Boltzmann – Volterra theory of hereditary creep.
ВВЕДЕНИЕ
Для многих твердых тел характерно изменение во времени напряженно-деформированного состояния при постоянной внешней нагрузке. Для конкретизации дальнейших выкладок в статье в качестве деформируемых твердых тел рассматриваются грунтовые основания, содержащие меловые отложения. Для исследования деформаций грунтов во времени при постоянной внешней нагрузке в настоящее время применяют теорию ползучести или теорию ползучести с одновременным учетом фильтрационной консолидации. Экспериментально доказано, что деформации скелета грунта могут быть описаны законом линейной наследственной ползучести Больцмана – Вольтерра [1–5]. Теория наследственной ползучести включает в себя все теории, базирующиеся на линейных реологических моделях. В силу указанной общности теории наследственной ползучести Больцмана – Вольтерра представляется возможным повысить точность исследования деформаций грунтовых оснований математическими методами.
В настоящей статье изложены результаты экспериментальных и теоретических исследований деформаций грунтовых оснований в соответствии с законом линейной наследственной ползучести Больцмана – Вольтерра, приведены разработанные реологическая математическая модель и приближенный аналитический метод исследования нелинейного деформирования неоднородного грунтового основания.
ДЕФОРМАЦИИ ГРУНТОВЫХ ОСНОВАНИЙ ФУНДАМЕНТОВ
Структура и свойства грунтовых оснований
По своей структуре и физико-механическим свойствам грунты являются сложными телами, которые включают в себя твердую, жидкую и газообразную фазы. Твердая фаза грунта (скелет) представляет пористую среду. Поры между твердыми частицами в грунте заполнены жидкостью (вода и водные растворы) и газом (воздух). Если поры в грунте заполнены целиком жидкостью (водонасыщенный грунт) или только газом (сухой грунт), то такие грунты называют двухфазными. Грунт называют трехфазным, если поры в нем содержат одновременно и воду и воздух. Двухфазные и трехфазные грунты воспринимают внешнюю нагрузку иначе, чем сплошные твердые тела. Распределение нагрузок в толще грунтов и их сопротивление внешним силам обусловлено силами сцепления и трения частиц грунта, а также сжатием поровой воды и ее выжиманием из пор. Сами частицы при этом практически не сжимаются, происходит только их сдвиг, вследствие чего уменьшаются поры в определенном объеме, и происходит сжатие и фильтрация поровой воды.
Движение поровой воды подчиняется законам фильтрации – закону Дарси. Указанные механические процессы обуславливают уплотнение грунта во времени – консолидацию. Фильтрационная консолидация оказывает значительное влияние на скорость нарастания деформации грунта под нагрузкой и поэтому не может рассматриваться отдельно от ползучести частиц, слагающих грунт. Степень общей консолидации грунта при действии на него внешней нагрузки определяет осадку фундамента на грунтовом основании [5–9].
Подходы к исследованию деформаций грунтовых оснований
Приведенные характеристики грунтов в целом дают возможность рассматривать грунтовые основания как произвольную неоднородную нелинейно деформируемую реологическую среду с произвольными законами деформирования любого ее элемента. Физическое состояние элементов структуры основания под нагрузкой описывается соответствующими уравнениями закона деформирования. Для элементов в стадии линейного деформирования это уравнение закона Гука. При нелинейном деформировании это будут более сложные формы зависимости напряжений и деформаций в каждом элементе. Учет уплотнения грунта во времени наиболее полно описывается интегральным уравнением. В границах деформируемой зоны будет некоторое количество структурных элементов с различными свойствами и связями между ними [10–15].
Следовательно, основание, фундамент и здание образуют единую систему, и ее исследование необходимо проводить в соответствии с принципами системного подхода. Такая система является очень большой и сложной, и поэтому ее исследование возможно только приближенными численными методами или численно с помощью современных ПЭВМ. Однако для оперативного принятия решения для задач данного класса получение приближенного аналитического решения представляет значительный интерес.
В настоящей статье в основу концептуальной модели системы основания и фундаментов положены следующие критерии:
1) основание, фундамент и здание рассматриваются как единая система;
2) основание по своей структуре и физико-механическим свойствам может быть произвольным. Все элементы структуры основания должны быть геометрически и физически описаны;
3) основание считается реологическим и нелинейно деформируемым;
4) форма, размеры и жесткость фундамента могут быть произвольными.
Таким образом, концептуальнаямодель системы представляется как конечная совокупность механико-математических моделей элементов системы. Ее исследование целесообразно проводить методами системного анализа [14].
В статье выбран именно такой подход: исходя из основных положений нелинейной деформируемости грунтов, фильтрационной консолидации и консолидации ползучести грунтов, исследуются осадки плитного фундамента на реологическом нелинейно деформируемом грунтовом основании.
О консолидации грунтовых оснований
По вопросам консолидации грунтов имеется обширная литература [2, 3, 6–12]. Следует отметить некоторые положения этой теории, необходимые для дальнейших выкладок при разработке механико-математических моделей и алгоритмов, определяющих реологические деформационные процессы грунтовых оснований фундаментов зданий.
Физические аспекты консолидации грунтов при приложении внешней нагрузки содержат следующие процессы: мгновенное сжатие ; фильтрационное уплотнение , обусловленное выжиманием воды из пор и ее фильтрацией; вторичная консолидация , иначе ползучесть скелета грунта, обусловленная невосстанавливающимися сдвигами частиц и их агрегатов.
В настоящее время существует несколько подходов к определению деформаций грунтов. В зависимости от конкретных условий применяют [1, 16]:
– теорию ползучести;
– теорию ползучести с одновременным учетом фильтрационной консолидации;
– теорию ползучести с одновременным учетом фильтрационной консолидации и сжимаемости поровой воды.
Представляет интерес сравнение этих подходов для конкретного грунтового материала. В [13] на рисунке 120 (рис. 1 в данной статье), приведены кривые консолидации и ползучести образца саратовской глины, рассчитанные: по теории чисто фильтрационной консолидации Терцаги – Герсеванова (см. рис. 1, кривая 1); по Флорину с учетом только ползучести скелета и фильтрационной консолидации грунта (кривая 2); с одновременным учетом фильтрационной консолидации, ползучести скелета грунта и сжимаемости поровой воды , т. е. как для трехфазной системы (кривая 3); полученные опытным путем (кривая 4).
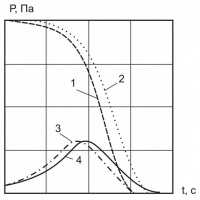
1 – рассчитанные по теории чисто фильтрационной консолидации Терцаги – Герсеванова; 2 – рассчитанные по Флорину с учетом только ползучести скелета и фильтрационной консолидации грунта; 3 – рассчитанные как для трехфазной системы; 4 – полученные опытным путем
Рис. 1. Кривые консолидации и ползучести образца саратовской глины (давление р = 0,20 Па; высота слоя h= 0,04 м; коэффициент относительной сжимаемости а0 = 0,00775 Па; коэффициент фильтрации кф = 12×10-8 м/с)
Приведенные данные указывают на огромное значение одновременного учета ползучести скелета грунта и сжимаемости поровой воды в процессе консолидации грунтов (см. рис. 1, кривые 3 и 4). В современной литературе термин «ползучесть» часто заменяют термином «вязкоупругость».
ИССЛЕДОВАНИЕ ДЕФОРМАЦИЙ ГРУНТОВЫХ ОСНОВАНИЙ МАТЕМАТИЧЕСКИМИ МЕТОДАМИ
Математическое моделирование грунтовых оснований
Математическая модель – это некоторый абстрактный образ, т. е. конечная совокупность логико-математических предложений, адекватно отображающих основные закономерности и особенности оригинала – реального объекта или системы, – которые имеют свою среду (пространство) и условия существования. Всякая реальная система или объект всегда имеют определенные связи с внешней средой, которая налагает свои условия на их существование и функционирование [11, 14]. Все эти и другие качества в математической модели должны иметь свое отображение, а это значит, что математическая модель может иметь свою структурную схему. В самом общем случае эта структурная схема может быть представлена следующим образом:
1) математическая модель среды существования системы или объекта;
2) математическая модель состояния среды системы;
3) условия связи моделируемой системы с внешней средой;
4) условия равновесия системы (ядро математической модели);
5) математическая модель результата решения.
Математическое наполнение элементов этой структуры зависит от класса моделируемых задач и даже от особенностей задач каждого класса. Предлагаемая структурная схема является общим эффективным алгоритмом построения математических моделей.
Учитывая произвольность постановки задачи, решать ее лучше методом математического моделирования на основе методов численного решения нелинейных краевых задач. Это сразу накладывает свои требования на структуру ядра математической модели. Будем строить его на основе одного из энергетических принципов, например, на основе принципа минимума полной потенциальной энергии системы. Математическая модель системы оснований и фундаментов в соответствии с приведенной структурой будет иметь вид согласно [14–16].
1. Схема геологического разреза основания.
2. Уравнение состояния элементов структуры грунтового основания:
(1)
3. Система краевых условий – определяются в соответствии с классификацией поставленной задачи как краевой задачи математической физики.
4. Условия равновесия системы (ядро математической модели):
5. Математическая модель (форма) искомого решения:
Математическое моделирование состояния вязкоупругих грунтовых оснований
Грунты деформируются как нелинейно упругопластические тела: вначале имеется почти линейный участок, потом нелинейный и далее пластическое состояние [5, 10, 11, 14, 15]. Уравнение состояния элементов структуры (слоев, включений и т. п.) грунтового основания при линейно упругой стадии работы имеет однозначное представление
(2)
В этом случае достаточно двух физико-механических характеристик: Е и m . Существует несколько хорошо отработанных методик их определения.
Для сложного напряженного состояния механико-математическая модель в общем виде может быть представлена так:
(3)
Для грунтов в настоящее время существует ряд конкретных форм закона деформирования. Наиболее простой из них и достаточно хорошо аппроксимирующей экспериментальные зависимости является степенная функция
(4)
Параметры А и m определяются экспериментально.
Повышение точности решения задач по расчету нелинейных деформаций может быть получено при применении модели закона деформирования в форме:
(5)
В теории упругости показано, что упругий изотропный материал характеризуется двумя упругими постоянными: модулем упругости и коэффициентом Пуассона или модулем сдвига и объемным модулем упругости.
Состояние изотропного вязкоупругого материала характеризуется сдвиговой и объемной ползучестью. В соответствии с экспериментальными данными С. Р. Месчана [1, 2, 13] предполагается, что скелет грунта изменяется в соответствии с законом линейной наследственной ползучести Больцмана – Вольтерра. Уравнение состояния в интегральной форме для среды, подчиняющейся этой теории, имеет следующий вид [1, 2, 4, 10, 13]:
(6)
где К (t , t ) – функция, называемая ядром ползучести . Эта функция характеризует собой реологические свойства рассматриваемой среды. Ядро К (t , t ) является положительной монотонно убывающей функцией своих аргументов;
s – полное напряжение;
e – деформация;
Е 0 – модуль деформации.
Если деформация e (t )известна, то уравнение (6) должно решаться относительно напряжения s (t ). B этом случае интегральное уравнение второго порядка (Вольтерра) получает следующий вид:
(7)
где R (t , t ) – функция, называемая ядром релаксации материала. Она является резольвентой ядра ползучести .
Теория ползучести, характеризуемая интегралом связи типа (6), носит наименование теории наследственности, так как она исходит из принципа соучастия предшествовавшего напряженного состояния и его влияния на действительное состояние.
Теория наследственной ползучести включает в себя все теории, базирующиеся на линейных реологических моделях.
Для внесения ясности в представление о природе ядра ползучести К (t , t ) необходимо напряжение в уравнении (6) принять постоянным, т. е. s (t ) = s 0 = const, и продифференцировать обе части уравнения по t :
(8)
Тогда функция К (t ) будет соответствовать скорости ползучести при единичной нагрузке, увеличенной в Е 0 раз.
Особые формы ядра ползучести имеют следующий вид:
1) для реологической модели Кельвина:
(9)
2) для логарифмического закона вторичной компрессии:
(10)
3) для комбинации из приведенных выше видов:
(11)
где d – коэффициент ядра ползучести;
d 1 – коэффициент затухания ползучести.
Коэффициенты d и d 1 определяются опытным путем в течение нескольких дней.
Далее в статье ядро ползучести строится в соответствии с реологической моделью Кельвина:
(12)
Интегральная форма уравнения деформирования в настоящей статье принята определяющей.
МЕТОДЫ ОПРЕДЕЛЕНИЯ РЕОЛОГИЧЕСКИХ ДЕФОРМАЦИЙ ГРУНТОВЫХ ОСНОВАНИЙ ФУНДАМЕНТОВ
Реологические линейно упругие деформации грунтовых оснований
Деформации грунтового основания большеразмерной фундаментной плиты, загруженной равномерной нагрузкой, имеют одну существенную особенность: горизонтальные составляющие перемещения в любых горизонтальных плоскостях в плане плиты значительно меньше вертикальной компоненты. Физически это легко обосновывается исходя из правила сложения векторов перемещений от действия системы сосредоточенных сил. Теоретически равенство нулю горизонтальных перемещений точек полупространства, загруженного равномерной внешней нагрузкой, можно доказать, используя решение Буссинеска задачи о действии сосредоточенной силы на поверхности этого полупространства. В механике грунтов аналитическое решение задачи об осадке загруженного слоя однородного грунта используется для решения отдельных задач. Для вертикальной компоненты вектора перемещения, т. е. для осадки равномерно загруженного слоя однородного грунтового основания, получено следующее выражение [5]
(13)
где b г = 1 - 2 m2г /(1 - m г);
Н – мощность деформируемого слоя;
q г –удельная нагрузка на поверхность грунтового основания;
m г – коэффициент Пуассона для грунтового основания;
Е г – модуль деформации грунта.
Это решение имеет место только для однородного основания. Однако приведенная формула может быть применена и к расчету многослойных оснований, в частности для грунтовых слоев с меловыми отложениями. Для этого необходимо рассматриваемому основанию поставить в соответствие однородное основание, геометрически равное исходному, но с модулем деформации и коэффициентом Пуассона такими, чтобы осадки загруженного слоя в обоих случаях были практически равными.
Из физического анализа рассматриваемого класса задач следует, что эквивалентный модуль деформации моделируемого однородного основания будет зависеть от метрических и физико-механических параметров слоев различной несущей способности и глубин их залегания. Следует также отметить, что в строительных нормах и правилах для задач рассматриваемого класса рекомендуется находить средневзвешенное значение модуля деформации. Это значит, что при наличии слоев пониженной или повышенной несущей способности глубина их залегания не учитывается, вносимая при этом погрешность в расчетах значительная. Поэтому необходимо учитывать не только мощность аномального слоя, но и глубину его залегания.
Приведенное решение может быть использовано для определения осадок жестких большеразмерных плит при действии на них равномерно распределенной внешней нагрузки. Но при этом необходимо учесть конечность размеров плиты, а рассматриваемое решение, как уже было указано, получено для условия равномерной загрузки всей поверхности полупространства.
Методом компьютерного объектно-ориентированного моделирования были исследованы указанные особенности при определении осадок жестких большеразмерных плит при действии на них равномерно распределенной внешней нагрузки. На основании результатов этого исследования для определения эквивалентного модуля деформации предлагается следующий алгоритм:
где Е ср – средний модуль деформации основания без учета слабого слоя;
Е экв – эквивалентный модуль деформации грунтового основания;
D Н – расстояние слабого слоя грунта от подошвы фундаментной плиты, при этом всегда D Н > 0;
D h , D hj – мощность слабого и других слоев грунта;
Е i , Е j – модуль деформации слабого и других слоев грунта;
m ср – средний коэффициент Пуассона;
m в – коэффициент Пуассона для выделяемого слоя.
При отсутствии выделяемого слоя грунта в толще грунтового основания D h = 0 и, следовательно, Е экв = Е ср.
Эквивалентный коэффициент Пуассона m экв определим исходя иззакона изменения объема, согласно которому модуль объемной деформации остается постоянной величиной как в пределах, так и за пределами упругости
Аналогично может рассматриваться любой аномальный слой, в частности меловые отложения.
При аналитическом определении осадки жесткой большеразмерной плиты на грунтовом основании, содержащем аномальный слой, необходимо ввести еще дополнительный коэффициент формы загруженной площадки b ф = 2 mэкв. Таким образом, для определения осадки жесткой фундаментной плиты получим следующее приближенное аналитическое выражение
(14)
где b экв= b г× bф;
q – среднее давление под плитой;
S – площадь плиты.
Компьютерное объектно-ориентированное моделирование деформаций основания большеразмерной фундаментной плиты при равномерной нагрузке на плиту для условий линейно упругого, нелинейно упругого и вязкоупругого деформирования грунта показало, что горизонтальные составляющие перемещения в любых горизонтальных плоскостях в плане плиты значительно меньше вертикальной компоненты: U = 0, V = 0, W ¹ 0; где U , V , W – горизонтальные и вертикальная составляющие вектора перемещения. Отсюда следует, что компоненты вектора деформаций будут равны:
(15)
Для анализа сдвиговых деформаций воспользуемся уравнениями равновесия в перемещениях, уравнениями Ламе, при статической нагрузке и без учета массовых сил:
Эти уравнения при учете (15) преобразуются к виду:
(16)
Отсюда следует, что компонента вертикального перемещения W большеразмерной фундаментной плиты не зависит от горизонтальных координат x и y . Следовательно, сдвиговые деформации будут равны:
Из последнего уравнения группы (16) следует
(17)
откуда
При линейно упругом деформировании значение константы с 0 может быть определено исходя из указанного выше решения Буссинеска. Тогда будем иметь:
(18)
В итоге получим выражение для определения осадки большеразмерной фундаментной плиты на упругом основании
(19)
что полностью соответствует (13).
Для сложного реологического линейно упругого основания необходимо определять Е экв и далее, согласно принципу Вольтерра и принятой формы ядра ползучести (12), в выражении (14) величину 1/ Е экв необходимо заменить на величину
Таким образом, для определения осадки большеразмерного плитного фундамента на реологическом линейно упругом основании будем иметь следующее приближенное выражение (инженерный метод):
(20)
где d , d 1 – экспериментальные величины.
Реологические нелинейно упругие деформации грунтовых оснований
Между интенсивностями деформаций при условии линейного и нелинейного деформирования твердого тела и при законе деформирования в виде степенной функции устанавливается следующая связь [14]:
(21)
где А , m – параметры уравнения состояния деформируемой среды:
(22)
Для рассматриваемой задачи из (21) при учете (15), (16) и ( 22) будем иметь:
(23)
где e , Н – индексы – признаки линейного и нелинейного деформирования.
Интегрируя (23) при учете (17) и (18), получим:
(24)
Таким образом, осадка большеразмерной фундаментной плиты на нелинейно деформируемом однородном основании нелинейно зависит от нагрузки, что полностью соответствует многочисленным экспериментальным данным.
Для сложного реологического основания необходимо определять А экв и далее согласно принципу Вольтерра в выражении (24) величину 1/ А экв необходимо заменить на величину
Таким образом, для определения осадки плитного фундамента на реологическом основании будем иметь следующее приближенное аналитическое выражение (инженерный метод):
(25)
Оценку точности полученных формул проведем на примере конкретной задачи.
Экспериментальные исследования деформаций оснований при учете фактора времени
Модельная задача № 1
На плитный фундамент размером 20х30 м и толщиной 0,4 м действует равномерно распределенная нагрузка интенсивностью q = 114,0 кПа. Модуль упругости плиты Е = 27×103 МПа, коэффициент Пуассона m = 0,29. Грунтовое основание представляет собой слой мергеля мощностью 6,5 м. Ядро релаксации имеет вид (12), где d = 0,5 1/сут, d 1 = 0,1 1/сут, Е = 9,0 МПа, m = 0,4.
При решении задачи методом конечных элементов рассматриваемая область дискретизировалась 7200 конечными элементами в форме треугольников. Временной шаг выбирался равным 0,5 суткам. Время нахождения решения на отрезке от 0 до 1000 суток составило менее 30 с. Стабилизированная осадка 5,55 см приходится на точку 395 сут [16].
Определим осадки, используя приближенные аналитические решения.
1) Грунтовое основание рассматривается как линейно упругая среда: мощность слоя H = 6,5 м, Е = 9,0 МПа, m = 0,4, удельная нагрузка q = 114,0 кПа.
Воспользуемся формулой (19):
где b = 1 - 2 m2/(1 - m ), P /S = q .
Произведя вычисления, получим W е = 3,87 см.
2) Грунтовое основание рассматривается как нелинейно упругая среда при приведенных характеристиках. Закон деформирования примем в форме степенной функции: s I = A e i m , A > 0, 0 < m < 1. Параметры закона деформирования определены по приближенным формулам [14], получено: m = 0,33, A = 1,30. Произведя вычисления по формуле (24), получим W н = 4,87 см.
3) Грунтовое основание рассматривается как реологическая линейно упругая среда при приведенных характеристиках.
Вычисления проведем по формуле (20). В этой формуле d , d 1 – экспериментальные величины, при этом получено: d = 0,5, d 1 = 0,1. Стабилизированная осадка Wt е = 5,45 см при t » 2 года.
4) Грунтовое основание рассматривается как реологическая нелинейно упругая среда при приведенных характеристиках.
Вычисления проведем по формуле (25). В этой формуле d , d 1 – экспериментальные величины, при этом получено: d = 0,4, d 1 = 0,1. Стабилизированная осадка Wt н = 5,8 см при t » 0,5 года.
Модельная задача № 2
На плитный фундамент площадью S = 5000 см2 (штамп) действует равномерно распределенная нагрузка интенсивностью q = 0,15 МПа. Грунтовое основание содержит меловые отложения с характеристиками: Е = (12–15) МПа, m = 0,4.
Ядро релаксации примем в виде (12), где d = 0,4 1/сут, d 1 = 0,1 1/сут.
Необходимо исследовать осадку плиты во времени при указанной нагрузке.
Решение задачи выполним, используя полученные приближенные аналитические решения. Мощность деформируемого слоя принята Н = 2 L = 200 см ( L = 100 см по условию).
1) Грунтовое основание рассматривается как линейно упругая среда.
Воспользуемся формулой (19):
где b = 1 - 2 m2/(1 - m ), Н = 200 см.
Произведя вычисления, получим W е = 0,59 см.
2) Грунтовое основание рассматривается как нелинейно упругая среда при приведенных характеристиках. Закон деформирования примем в форме степенной функции: s I = A e i m , A > 0, 0 < m < 1. Параметры закона деформирования определены по приближенным формулам [14], получено: m = 0,33, A = 0,98. Произведя вычисления по формуле (24), получим W н = 0,81 см.
3) Грунтовое основание рассматривается как реологическая линейно упругая среда при приведенных характеристиках.
Вычисления проведем по формуле (20). В этой формуле d , d 1 – экспериментальные величины, при этом получено: d = 0,5, d 1 = 0,1. Стабилизированная осадка Wt е = 0,68 см при t » 2 года.
4) Грунтовое основание рассматривается как реологическая нелинейно упругая среда при приведенных характеристиках.
Вычисления проведем по формуле (25). В этой формуле d , d 1 – экспериментальные величины, при этом получено: d = 0,5, d 1 = 0,1. Стабилизированная осадка Wt н = 0,95 см при t » 2 года.
Сравнительный анализ деформаций реологических грунтовых оснований теоретическими и экспериментальными методами
Вследствие анализа результатов решения модельных задач можно сделать следующие выводы:
1. Решение модельной задачи № 1, полученное по разработанным формулам, хорошо согласуется с решением, полученным методом компьютерного моделирования.
2. Решение модельной задачи № 2, полученное по разработанным формулам, хорошо согласуется с результатами соответствующего натурного эксперимента, полученными в отделе оснований и фундаментов РУП «Институт БелНИИС».
В целом анализ результатов исследования деформаций реологических линейно упругих и нелинейно упругих грунтовых оснований показывает возможность практического применения разработанного приближенного аналитического (инженерного) метода для расчета осадок фундаментов на грунтовых основаниях указанного типа.
ЗАКЛЮЧЕНИЕ
1 В настоящей статье методами натурного физического эксперимента и математического моделирования с учетом фильтрационной консолидации и консолидации ползучести грунтов исследовались осадки плитного фундамента на грунтовых основаниях, содержащих меловые отложения.
2 В плане рассматриваемой темы сформирована система исследования, проведен анализ элементов ее структуры, построена механико-математическая модель реологической системы, разработан приближенный аналитический метод ее исследования. Для учета деформирования реологического основания использована интегральная форма закона деформирования. Разработан алгоритм инженерного метода расчета осадки плитного фундамента на реологическом грунтовом основании.
3 Полученные результаты могут быть использованы при расчетах осадок плитных фундаментов на реологических грунтовых основаниях произвольной структуры.
СПИСОК ЛИТЕРАТУРЫ
1. Алексан дров, А. В. Основы теории упругости и пластичности / А. В. Александров, В. Д. Потапов. – М.: Высшая школа, 1990. – 400 с.
2. Вялов, С. С. Реологические основы механики грунтов / С. С. Вялов. – М.: Высшая школа, 1978. – 446 с.
3. Зарецкий, Ю. К. Теория консолидации грунтов / Ю. К. Зарецкий. – М.: Наука, 1967. – 320 с.
4. Шукле, Л. Реологические проблемы механики грунтов / Л. Шукле.– М.: Стройиздат, 1976. – 486 с.
5. Цытович, Н. А. Механика грунтов / Н. А. Цытович. – М.: Высшая школа, 1973. – 280 с.
6. Малинин, Н. Н.. Прикладная теория пластичности и ползучести / Н. Н. Малинин. – М.: Машиностроение, 1976. – 400 с.
7. Победря, Б. Е. Численные методы в теории упругости и пластичности / Б. Е. Победря. – М.: Издательство Московского университета, 1981. – 344 с.
8. Рейнер, М. Реология / М. Рейнер. – М.: Наука, 1965. – 280 с.
9. Ржаницын, А. Р. Теория ползучести / А. Р. Ржаницын. – М.: Стройиздат, 1968. – 416 с.
10. Старовойтов, Э. И. Основы теории упругости, пластичности и вязкоупругости / Э. И. Старовойтов. – Гомель: БелГУТ, 2001. – 344 с.
11. Журавков, М. А. Математическое моделирование деформационных процессов в твердых деформируемых средах / М. А. Журавков. – Минск: БГУ, 2002. – 456 с.
12. Амусин, Б. З. Метод конечных элементов при решении задач горной геомеханики / Б. З. Амусин, А. Б. Фадеев. – М.: Недра, 1975. – 144 с.
13. Фадеев, А. Б. Метод конечных элементов в геомеханике / А. Б. Фадеев. – М.: Недра, 1987. – 224 с.
14. Быховцев, В. Е. Компьютерное моделирование систем нелинейной механики грунтов / В. Е. Быховцев, А. В. Быховцев, В. В. Бондарева. – Гомель: Гомельский государственный университет им. Ф. Скорины, 2002. – 215 с.
15. Быховцев, В. Е. Механико-математическая модель деформирования грунта при его уплотнении и упрочнении / В. Е. Быховцев, В. В. Бондарева, Л. А. Цурганова // Известия Гомельского государственного университета им. Ф. Скорины. – 2003. – № 5. – С. 136–139.
16. Быховцев, В. Е. Интегральный метод построения математической модели и алгоритма исследования вязкоупругих деформаций грунтовых оснований / В. Е. Быховцев, К. С. Курочка, В. Е. Сеськов // Вестник БНТУ. – 2008. – № 4. – С. 17–24.


